Como plataformas de ensino virtuais estão transformando a educação
Nos últimos anos, foi imensa a quantidade de mudanças que a tecnologia promoveu na sociedade. A evolução tecnológica vem transformando a saúde, a economia e a comunicação, por exemplo. Uma das áreas mais positivamente influenciadas pela tecnologia é a educação. Atualmente há diversas plataformas de ensino virtuais que estão alterando profundamente a educação no Brasil […]
Resumo Teórico – Conceito de Função
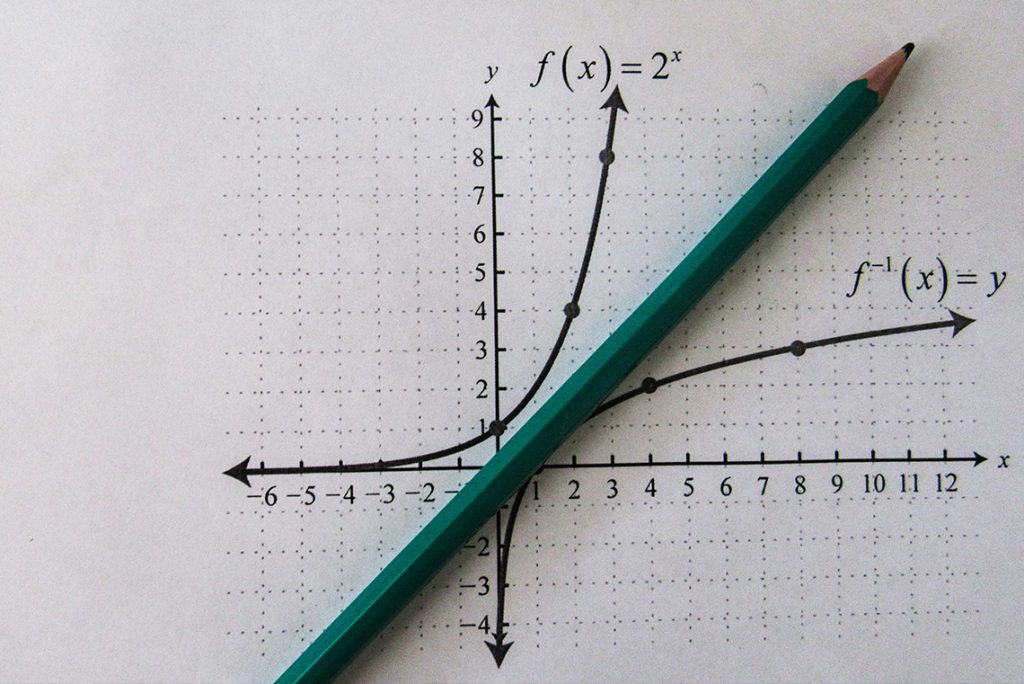
Nest post vamos fazer um resumo teórico introduzindo o conceito de função. Vamos usar muitos conceitos apresentados no post de Conjuntos, Variáveis e Equações e do post de Reta Numérica e Par Ordenado! Vamos nessa! Definição Uma função f é uma lei (relação) que faz cada elemento x de um conjunto A corresponder a um […]
Resumo Teórico – Plano Cartesiano e Pares Ordenados
Neste post, vamos fazer um resumo teórico sobre o Plano Cartesiano e Pares Ordenados. Vamos usar o conhecimento adquirido no post sobre Reta Numérica. Se não conferiu ainda, você confere aqui. Plano Cartesiano O Plano Cartesiano (nome dado em homenagem ao matemático e filósofo francês – René Descartes) é um sistema de referência formado por duas […]
O papel da família na aprovação #06
Confira como a Ingrid venceu o desafio de passar no vestibular da USP, e entenda como o apoio incondicional da família dela foi um ponto muito importante para realizar esse sonho.
O papel da família na aprovação #03
Confira o que a família do nosso aluno aprovado Felipe Bomfim, contou sobre a decisão dele de focar 100% nos estudos para ser aprovado.
O papel da família na aprovação #02
Confira nesse vídeo como o suporte da família foi importante na aprovação do Bruno Lanza na AFA.




