Resumo Teórico – Função do Primeiro Grau e seu Gráfico – Parte 1
Neste post, vamos fazer um resumo teórico sobre função do primeiro grau, explicando o que são seus coeficientes e o formato geral do seu gráfico! Se você não conferiu os posts sobre Variáveis, Equações, Reta Numérica e Função, vá lá no blog e confira! Definição Uma função do primeiro grau é toda equação que pode […]
Resumo Teórico – Conceito de Função
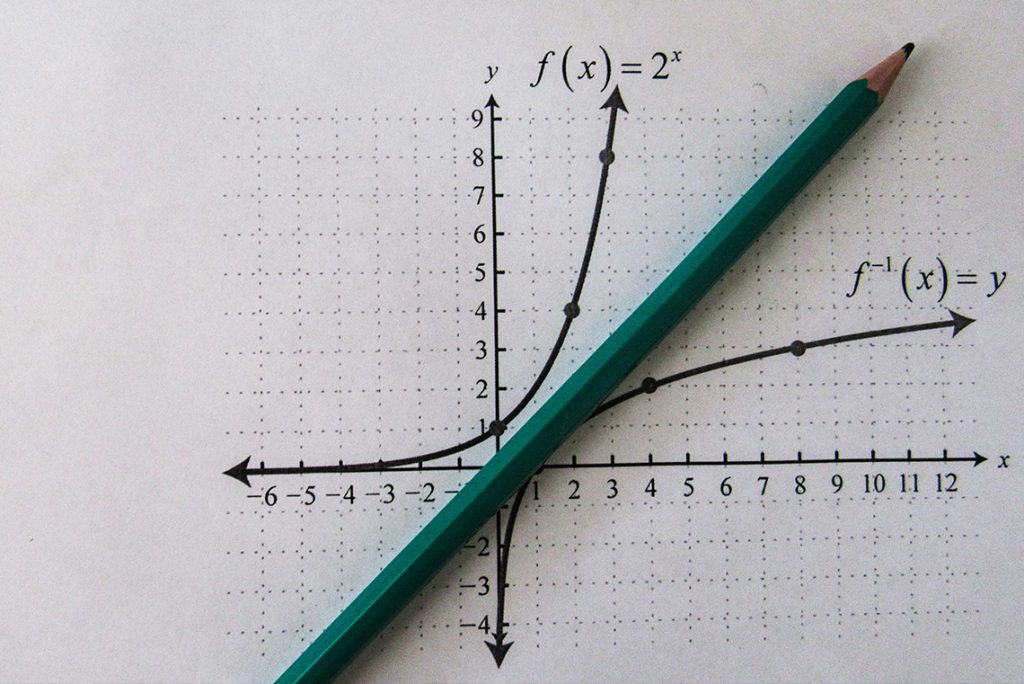
Nest post vamos fazer um resumo teórico introduzindo o conceito de função. Vamos usar muitos conceitos apresentados no post de Conjuntos, Variáveis e Equações e do post de Reta Numérica e Par Ordenado! Vamos nessa! Definição Uma função f é uma lei (relação) que faz cada elemento x de um conjunto A corresponder a um […]




