Resumo de fisica: Colisões e centro de massa II

COLISÕES MECÂNICAS COM SUPERFÍCIES PLANAS

• Quando a colisão é perpendicular à superfície plana, a variação de velocidade acaba sendo uma soma modular dos valores das velocidades inicial e final.

A variação da velocidade é a velocidade final menos a velocidade inicial, mas como essas duas velocidades têm a mesma direção e sentidos opostos, fica: “a variação da velocidade é a final menos menos a inicial, o que dá final mais inicial. Por exemplo, a bola da figura chega com 4m/s e volta depois de bater na parede com 2m/s, o que gera uma variação de velocidade nessa direção de 6m/s!! Lembrar que no caso o sistema bola não é isolado, então devemos usar o teorema do impulso para calcular forças médias e tempos de interação da bola com a parede:

$F\cdot \Delta t = m\cdot \Delta v$

• Cálculo do coeficiente de restituição: o coeficiente de restituição de velocidade relativa é a intensidade da velocidade relativa após a colisão pela intensidade da velocidade relativa antes da colisão. No caso acima, por exemplo, teríamos para a colisão horizontal da bola de futebol com a parede:

$e = \frac{V_{rel af}}{V_{rel apr}} = 2-0/4-0 = 2/4 = 0,5 = 50\%$

isto é, houve restituição de 50% da velocidade relativa.

• Para uma bola que é abandonada de uma altura h 1 , colide com o chão e retorna para uma altura menor h 2 , temos para a descida:

$m\cdot g\cdot h_{1} = \frac{m\cdot v_i^{2}}{2}$

logo

$v_{i} = \sqrt{2\cdot g\cdot h_{1}}$

e podemos fazer o mesmo para a subida imediatamente depois da colisão, o que resulta

$v_{f} = \sqrt{2\cdot g\cdot h_{2}}$

Logo o coeficiente de restituição será

$e = \sqrt{\frac{h_{2}}{h_{1}}}$

COLISÕES OBLÍQUAS COM SUPERFÍCIES PLANAS

Quando temos uma colisão diagonal de uma bolinha de massa m em uma parede plana de massa infinita devemos perceber que na direção do eixo x, perpendicular à parede não há conservação de quantidade de movimento, e:

$F_{parede}\cdot \Delta t = \Delta Q.$

E na direção y, paralela à parede, não há forças trocadas, portanto, há conservação da quantidade de movimento.

Claro que nesse caso, estamos desprezando forças de atrito da bolinha com a parede.

Na direção do eixo x:

$F\cdot \Delta t = m\cdot v_{f} \cdot cos\theta - m\cdot v_{i}\cdot cos\theta$

Na direção do eixo y:

$F_{y} =0$

logo

$m\cdot v_{i}\cdot sen \theta = m\cdot v_{f} \cdot sen\theta$

o que nos leva a

$V_{i} =V_{f}$

supondo que a massa seja sempre constante.

COLISÕES ELÁSTICAS BIDIMENSIONAIS

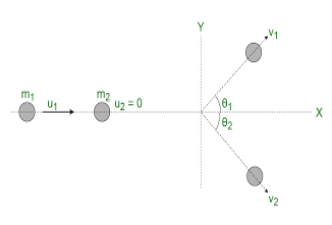
Quando temos uma colisão elástica bidimensional devemos decompor o problema em duas direções perpendiculares, x e y da figura. O sistema é isolado, isto é, não há a ação de forças externas, logo o momento linear ou quantidade de movimento se conservam antes e depois da colisão, e a energia cinética total antes e depois da colisão se conserva também.

Conservação da quantidade de movimento:

Na direção x:

$m_{1}\cdot u_{1}+m_{2}\cdot u_{2} = m_{1}\cdot v_{1}\cdot cos \theta _{1}+m_{2}\cdot v_{2}\cdot cos \theta _{2}$

mas

$u_{2} = 0$

logo:

$m_{1}\cdot u_{1}= m_{1}\cdot v_{1}\cdot cos \theta _{1}+m_{2}\cdot v_{2}\cdot cos \theta _{2}\;\;(I)$

Na direção y não há quantidade de movimento no início na mvertical, logo:

$0 = m_{2}\cdot v_{1}\cdot sen\theta _{1} - m_{2}\cdot v_{2}\cdot sen \theta _{2}$

o que nos leva a:

$m_{1}\cdot v_{1}\cdot sen\theta _{1}=m_{2}\cdot v_{2}\cdot sen \theta _{2}\;\;(II)$

E conservando a energia cinética temos:

$\frac{m_{1}\cdot u_{1}^{2}}{2}=\frac{m_{1}\cdot v_{1}^{2}}{2}+\frac{m_{2}\cdot v_{2}^{2}}{2}$

o que nos leva a:

$m_{2}\cdot u_{1}^{2} = m_{1}\cdot v_{1}^{2}+m_{2}\cdot v_{2}^{2}\;\;(III)$

A solução do sistema formado pelas equações I, II e III nos permite calcular as velocidades e energias desconhecidas.

CENTRO DE MASSA: SISTEMA MECANICAMENTE ISOLADO

Em sistemas mecanicamente isolados, isto é, sem a atuação de forças externas e impulsos externos, tais como explosões e colisões, a quantidade de movimento se conserva, a aceleração do centro de massa é nula, a variação da velocidade do centro de massa é nula, isto é, a velocidade do centro de massa é constante, não se altera. Se além disso o centro de massa estiver inicialmente parado isso significa que sua velocidade é nula e continuará nula, mantendo o centro de massa imóvel na ausência de forças externas.

Lembrar que o centro de massa é o ponto do espaço que possui propriedades mecânicas como se toda a matéria e a massa do corpo estivessem concentradas ali.

Ex₁: Quando um canhão atira uma bala para a frente e recua com uma velocidade menor que a bala, na medida que sua massa é maior que a da bala, isso ocorre pois o sistema é isolado e o centro de massa deve ser imóvel, o que significa deslocamento menor para a maior massa e maior para a menor massa. Isto é, a conservação da posição e velocidade do centro de massa de um sistema de partículas pode ser explicado ou por ação e reação, ou por conservação do momento linear.

Ex₂: Uma pessoa de massa m percorre de uma ponta a outra uma prancha horizontal de massa M que pode se mover sobre o chão sem atrito. O tamanho da prancha é L e a velocidade da pessoa em relação à prancha é u. Qual o deslocamento da pessoa em relação ao chão?

• Pela conservação da quantidade de movimento temos:

$m\cdot (u-V)-M\cdot V = 0$