Resumo de matematica: Estudo Geral das Funções I
Introdução e propriedades gerais
Definição: Dados dois conjuntos e
, não vazios, uma relação
de
em
recebe o nome de função de
em
se, somente se, para todo
existe só um
tal que
.
Exemplos
a) A relação é uma função.
b) A relação não é uma função, pois existe um elemento de
que não está relacionado com nenhum elemento de
.
c) A relação não é uma função, pois existe um elemento de
que está relacionado com dois elementos de
.
Observe as seguintes funções as seguir:
a) A função está definida de
em
.
Assim,
b) Ao programar uma fórmula na planilha de cálculo, Arthur pretendia que ela fornecesse o dobro de um valor dado. Mas na elaboração da fórmula, ele cometeu um erro, conforme mostram os primeiros resultados que apareceram na tabela:
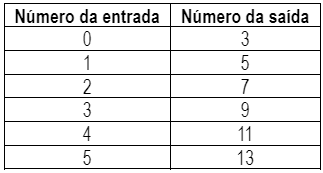
Considerando x o número de entrada e y o número de saída da fórmula digitada por Arthur, logo, a modelagem da relação pode ser obtida da seguinte forma:
Introdução e propriedades gerais - Outros exemplos
Considere os conjuntos e
, determine:
a) (Produto Cartesiano)
b) (Relação Binária)
Para
Para
Para
c) (Função)
Para
Para
Para
Nota
Dados dois conjuntos e
, não vazios, uma relação
de
em
recebe o nome de função de
em
se, somente se, para todo
existe só um
tal que
.
OBSERVAÇÕES
I) Toda função é uma relação, mas a recíproca não é verdadeira;
II) As funções são representadas por letras latinas minúsculas: ;
III) O domínio de uma função é sempre o próprio conjunto de partida;
IV) Sendo uma função definida de A em B, usamos a seguinte notação:
(lê-se: f é uma função de A em B)
Exemplo:
Observe que o valor de depende do valor de
, ou seja,
é uma função de
.
Dizemos que é a variável independente e
, a variável dependente.
Retomando o exemplo anterior, temos que:
Valor numérico
O valor numérico de , para
, na função
, é o valor obtido quando substitui-se
por a e realizam-se os devidos cálculos.
Exemplos
a) Sendo , definida por
, temos que:
;
;
.
Portanto, os valores numéricos de e
são, respectivamente,
e
.
b) Considere a função , definida de
em
, temos:
Analisando o diagrama de flechas podemos concluir que:
a) f)
, para
b) g)
, para
ou
c) h)
d) i)
, para
ou
e) j)
,
não está definido em
.
c) Sendo uma função real, tal que
e
. Determine o valor de
.
Assim,
Valor numérico - Outros exemplos
Numa função , tem-se que para algum
, se
, então a será raiz da função
.
Exemplo:
Considere a função real . Determine a raiz de
.
Para encontrar a raiz de , tem-se que
. Logo,
Portanto, 2 é raiz de .
Outros exemplos sobre valor numérico
Ex 1: Seja a função de
em
definida por
. Qual é o elemento do domínio que tem
como imagem?
Resolução:
Para determinar o valor de do domínio que tem imagem
basta fazer
.
Ex 2: (Unesp) Uma função de variável real satisfaz a condição , qualquer que seja o valor da variável
. Sabendo-se que
, determine o valor de:
a)
b)
Resolução:
a) Para :
b) Para x = 3:
Ex 3: A função de
em
é tal que, para todo
,
. Se
, calcule
.
Fazendo
Fazendo
Portanto, .
Domínio Algébrico de uma função real
Toda função é formada por três elementos: Domínio, Contradomínio e Imagem. Escrevendo f de forma algébrica, devemos determinar os possíveis valores de
, sendo
elemento do domínio e este, um subconjunto de
.
Exemplos:
a)
Condição de existência
Portanto, .
b)
Condição de existência
e
Portanto, ou
c)
Condição de existência
Portanto, .
Aplicações
Domínio algébrico de uma função real – RESUMO
(1° CASO) Função sem radical
Atenção: O denominador de uma fração qualquer deve ser sempre diferente de zero
(2° CASO) Função com radical
Atenção
Quando o índice de uma raiz for ímpar, o radicando poderá ser qualquer número real, bastando apenas analisar o fato de estar ou não no denominador de uma fração. Mas, quando o índice de uma raiz for par, o radicando só poderá ser maior ou igual a zero, bastando apenas analisar o fato do mesmo estar no denominador de uma fração, sendo nesse caso apenas maior que zero.
Exemplos:
a)
Nessa situação, para real implica numa imagem
também será real.
Portanto, .
b)
Condição de existência
Portanto,
c)
Nessa situação, para real implica numa imagem
também será real. Isso se deve ao fato de que a raiz de índice ímpar que aparece no numerador não possui restrição e que o denominador não tem como ser zero para qualquer
real.
Portanto, .
d)
Condição de existência
Portanto, .
e)
Condição de existência
Portanto, .






