Resumo de matematica: Probabilidade I
Experimento Aleatório, Espaço Amostral e Evento
1. EXPERIMENTO ALEATÓRIO
Algumas perguntas podem ser respondidas se forem conhecidas certas condições, como por exemplo, a que distância do solo um objeto começa a atingir uma temperatura de 200° C? ou qual a velocidade que um carro desenvolver para percorrer uma determinada distância num certo intervalo de tempo?
Esses experimentos são denominados determinísticos, pois podem ser previstos, caso contrário, o mesmo será chamado de experimento aleatório.
Um experimento será aleatório se, somente se, seus resultados dependam exclusivamente do acaso mesmo que sejam repetidos inúmeras vezes e conhecido todas os possíveis resultados. Como não podemos prever o resultado de um experimento aleatório, procuraremos descobrir as possibilidades de ocorrência de cada um.
A teoria da probabilidade surgiu para tentar medir a “chance” de ocorrer um determinado resultado num experimento aleatório.
Exemplos
a) No lançamento de uma moeda, qual a face voltada para cima?
b) No lançamento de um dado, que número saiu?
c) Uma carta foi retirada de um baralho completo. Que carta foi essa?
Atenção
Quando num experimento aleatório todos os resultados possíveis tiverem a mesma “chance” de ocorrer chamaremos de experimento aleatório equiprovável. Caso contrário, o experimento será chamado de “viciado”.
2. ESPAÇO AMOSTRAL (U)
O conjunto de todos os resultados possíveis de um experimento aleatório é denominado espaço amostral. O espaço amostral também poderá ser chamado de conjunto universo e seu número denotado por n(U).
Exemplos
a) No lançamento de uma moeda, e
.
b) No lançamento de um dado,e
.
3. EVENTO (E)
É qualquer subconjunto pelos elementos de um espaço amostral. Os eventos poderão ser chamados de resultados favoráveis do conjunto universo e seu número será dado por n(E).
Exemplo
Duas moedas são lançadas para cima e observa-se as faces voltadas para cima. Determine os eventos a seguir:
Considere C: cara e K: coroa
a) as faces serem iguais.
b) as faces terem pelo menos uma cara.
Análise do espaço amostral e evento
1. ESPAÇO AMOSTRAL (U)
O conjunto de todos os resultados possíveis de um experimento aleatório é denominado espaço amostral. O espaço amostral também poderá ser chamado de conjunto universo e seu número denotado por n(U).
Exemplos
a) No sorteio da mega sena, e
.
b) Numa caixa com 7 bolas diferentes, retirar duas é .
c) Num grupo de 10 pessoas, escolher 3 para formar um pódio é .
2. EVENTO (E)
É qualquer subconjunto pelos elementos de um espaço amostral. Os eventos poderão ser chamados de resultados favoráveis do conjunto universo e seu número será dado por n(E).
Exemplos
1. Um dado com 6 faces numeradas de 1 a 6 é lançado para cima e observa-se a face voltada para cima. Determine os eventos a seguir:
a) a face ser um número par.
b) a face ser um número primo.
c) a face ser menor que 5.
d) a face ser o número 8.
e) a face ser menor que 7.
OBSERVAÇÕES
Se o evento for um conjunto vazio, então o mesmo será chamado de evento impossível. Se o evento e o espaço amostral forem conjuntos iguais, então o evento será chamado de evento certo.
2. Um casal planeja ter três filhos. Determine os seguintes eventos:
a) que apenas dois sejam meninos.
b) que os 3 filhos sejam do mesmo sexo.
3. Uma pedra do jogo de dominó é retirada de dentro de uma caixa. Determine os eventos:
a) que os dois números iguais.
b) que a soma dos números seja 6.
Cálculo da probabilidade de um evento e propriedades
PROBABILIDADE
Se, num experimento aleatório, o número de elementos do espaço amostral é
e o número de elementos do evento
é
, então a probabilidade de que ocorra o evento
é dada por pelo número real
, tal que:
: número de resultados favoráveis
: número total de resultados possíveis
PROPRIEDADES
. Se
, então
e
.
. Se
, então
e
.
. Se
, então
.
. Se
e
são eventos complementares, então
.
Cálculo da probabilidade - Outros exemplos
OBS 1: Na resolução das questões de probabilidade é importante determinar a quantidade de elementos do espaço amostral ou até mesmo descrever esse conjunto para buscar dentro desse conjunto a característica “evento” solicitada.
OBS 2: Sabe-se que , sendo
o conjunto evento e
o espaço amostral. Assim, as informações (“características”) serão retiradas do espaço amostral.
OBS3: O espaço amostral no lançamento de dois dados simultâneos ou um após o outro terá 36 possibilidades. Essas possibilidades podem ser observadas na disposição de pares ordenadas.
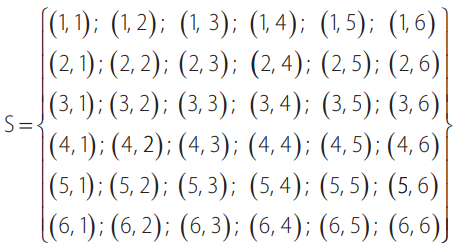
Aplicações I
OBS 1: A probabilidade funciona como uma razão e assim, seu resultado pode ter infinitas outras razões equivalentes. Deve-se ter atenção para analisar os elementos da razão e poder concluir sobre o que se pede.
, com
e
.
OBS 2: A probabilidade relacionando pontos de uma região será calculada a partir do contexto. Utilizar o perímetro da figura ou até mesmo a área limitada por esse perímetro são algumas das formas de abordagem desse tema, então ficar atento em como calcular esses elementos dessas regiões é essencial para sua solução.
OBS 3: O cálculo de possibilidades que satisfazem a uma certa característica é um hábito essencial no estudo das probabilidades, então a escolha da Análise Combinatória como estratégia para determinar essas quantidades é bastante interessante.
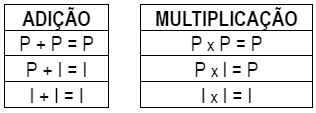
OBS 4: Considere e
sendo um número par e
, um número ímpar. Assim, no conjunto dos números naturais podemos garantir que:
Aplicações II
OBS 1: O cálculo de possibilidades que satisfazem a uma certa característica é um hábito essencial no estudo das probabilidades, então a escolha da Análise Combinatória como estratégia para determinar essas quantidades é bastante interessante.
OBS 2: Muitos problemas de contagem aparecem como melhor opção para resolução a utilização do evento complementar. A solução se torna mais rápida e eficaz, visto que não existe a necessidade de determinação de todos os eventos com tal característica.
OBS 3: O cálculo de possibilidades de um objeto geométrico por vezes se torna mais eficiente quando ocorre a análise por partes. Como por exemplo, tem-se que a escolha de três vértices de uma mesma face do cubo. A ideia é começar por uma face e, em seguida, ampliar o raciocínio para as outras faces.
Esse número pode ser assim calculado como: , sendo 6 faces e
a quantidade de escolhas de 3 vértices entre 4 de uma mesma face.
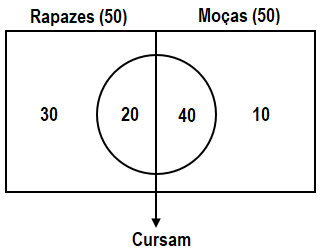
OBS 4: A escolha da estratégia do “campo de futebol” para organizar duas características sobre um mesmo universo além de ser bastante prática é também didática.
Exemplos de organização
1. Estratégia de tabela
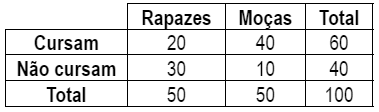
2. Estratégia do “campo de futebol”