Resumo de matematica: Trigonometria - Equações e Inequações

Equações Fundamentais - 0 a $2\pi$

Para a solução de equações trigonométricas, precisamos tentar chegar em uma das equações fundamentais, que são:

$sen(\alpha )=sen(\beta )$
$cos(\alpha )=cos(\beta )$
$tg(\alpha )=tg(\beta )$

A partir daí, se pertence a um dos quadrantes, ou seja, se não pertence às extremidades dos eixos coordenados, vamos ter sempre duas soluções no intervalo $[0,2\pi ]$ .
No caso do seno, essas soluções são pares do 1º e 2º quadrantes ou do 3º e 4º quadrantes, pois seno é positivo para “cima” e negativo para “baixo” do eixo x.
No caso do cosseno, os pares serão do 1º e 4º quadrantes (onde o cosseno é positivo) ou do 2º e 3º quadrante (onde o cosseno é negativo).
Já para a tangente, os pares serão do 1º e 3º quadrantes (onde a tangente é positiva) ou 2º e 4º quadrantes (onde a tangente é negativa).

Equações Fundamentais - Reais

Para equações trigonométricas nas quais as incógnitas (arcos) pertencem ao conjunto dos números reais, não podemos deixar de acrescentar $2k\pi$ na solução encontrada para a primeira volta no ciclo trigonométrico. Isso ocorre porque qualquer arco côngruo a um arco da solução, também é solução, já que nosso conjunto universo é dos Reais.

No caso especial da tangente, as raízes aparecem sempre “de meia em meia volta”, o que significa que podemos usar a menor das soluções na primeira volta do ciclo trigonométrico e ao invés de adicionarmos $2k\pi$ , devemos utilizar $k\pi$ .

Exemplos.

Para a solução de equações trigonométricas com mais de uma função, devemos tentar escrever todas as funções em função de apenas uma. Por exemplo, se $\alpha \,\epsilon \,[0,2\pi ]$ , resolva a equação

$sen^2(x)+cos(x)+1=0$

Solução:
Inicialmente, devemos escrever todas as funções trigonométricas em função de apenas uma. Com isso, faremos

$sen^2(x)=1-cos^2(x)$

Temos, assim

$1-cos^2(x)+cos(x)+1=0$
$-cos^2(x)+cos(x)-2=0$
$cos^2(x)-cos(x)+2=0$

Resolvendo esta equação do 2º grau, chegamos a $cos(x)=2$ (não convém) e $cos(x)=-1$ , donde concluímos que $x=\pi$

Inequações Fundamentais

A solução de inequação trigonométrica, envolve necessariamente um estudo no ciclo trigonométrico, no qual deve existir uma correspondência entre intervalos nos eixos (dos cossenos, dos senos, das tangentes) e arcos. Por exemplo, qual a solução da inequação $sen(x)\leq -\frac{1}{2}$ , sendo x $x\,\epsilon \,\left [ 0,2\pi \right ]$ ?

Solução:

Analisando o eixo dos senos, a solução que procuramos está relacionada ao intervalo em destaque:

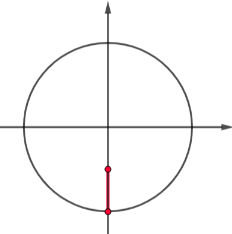
O conjunto de pontos da circunferência trigonométrica que correspondem ao segmento destacado são:

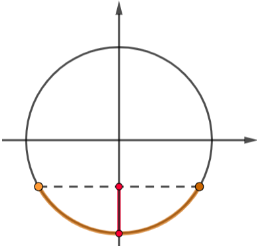
Como $sen(30^{\circ})=\frac{1}{2}$ , então as extremidades da solução são os arcos simétricos ao $30^{\circ}$ no 3º e 4º quadrantes, ou seja,

$210^{\circ}\leq x\leq 330^{\circ}$

Exercícios Resolvidos

Vamos resolver o problema: Para que valores de $x\,\epsilon\, \left [ 0,2\pi \right ]$ , $cos(2x)> 2 sen(x)+2$ ?
Inicialmente, precisamos tentar colocar todas as funções em função de apenas uma delas.

Solução:

Como $cos(2x)=1-sen^2(x)$ , temos:

$cos(2x)> 2sen(x)+2$
$1-sen^2(x)> 2sen(x)+2$
$sen^2(x)+ 2sen(x)+1>0$
$(sen(x)+1)^2>0$

Temos um quadrado positivo, ou seja, o único valor que não devemos aceitar para $sen(x)$ é $\frac{3\pi }{2}$ . Portanto, $x\,\epsilon \,[0,2\pi]-\frac{3\pi}{2}$ .